Implement Stack using Queues

-

We are given a Queue data structure that supports standard operations like enqueue() and dequeue(). We need to implement a Stack data structure using only instances of Queue and queue operations allowed on the instances

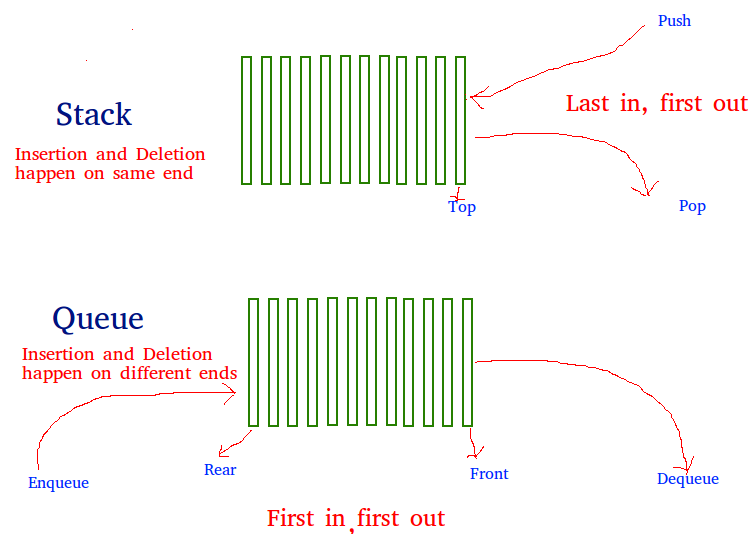
Stack and Queue with insert and delete operations

A stack can be implemented using two queues. Let stack to be implemented be ‘s’ and queues used to implement be ‘q1’ and ‘q2’. Stack ‘s’ can be implemented in two ways:

Method 1 (By making push operation costly)
This method makes sure that newly entered element is always at the front of ‘q1’, so that pop operation just dequeues from ‘q1’. ‘q2’ is used to put every new element at front of ‘q1’.

  1. push(s, x) operation’s step are described below:
    • Enqueue x to q2
    • One by one dequeue everything from q1 and enqueue to q2.
    • Swap the names of q1 and q2
  2. pop(s) operation’s function are described below:
    • Dequeue an item from q1 and return it.

Below is the implementation of the above approach:

/* Java Program to implement a stack using 
two queue */
import java.util.*;
 
class GfG {
 
    static class Stack {
        // Two inbuilt queues
        static Queue<Integer> q1 = new LinkedList<Integer>();
        static Queue<Integer> q2 = new LinkedList<Integer>();
 
        // To maintain current number of
        // elements
        static int curr_size;
 
        Stack()
        {
            curr_size = 0;
        }
 
        static void push(int x)
        {
            curr_size++;
 
            // Push x first in empty q2
            q2.add(x);
 
            // Push all the remaining
            // elements in q1 to q2.
            while (!q1.isEmpty()) {
                q2.add(q1.peek());
                q1.remove();
            }
 
            // swap the names of two queues
            Queue<Integer> q = q1;
            q1 = q2;
            q2 = q;
        }
 
        static void pop()
        {
 
            // if no elements are there in q1
            if (q1.isEmpty())
                return;
            q1.remove();
            curr_size--;
        }
 
        static int top()
        {
            if (q1.isEmpty())
                return -1;
            return q1.peek();
        }
 
        static int size()
        {
            return curr_size;
        }
    }
 
    // driver code
    public static void main(String[] args)
    {
        Stack s = new Stack();
        s.push(1);
        s.push(2);
        s.push(3);
 
        System.out.println("current size: " + s.size());
        System.out.println(s.top());
        s.pop();
        System.out.println(s.top());
        s.pop();
        System.out.println(s.top());
 
        System.out.println("current size: " + s.size());
    }
}
// This code is contributed by Prerna

Output :

current size: 3321current size: 1

Way 2 (By making pop operation costly)
In push operation, the new element is always enqueued to q1. In pop() operation, if q2 is empty then all the elements except the last, are moved to q2. Finally the last element is dequeued from q1 and returned.

  1. push(s, x) operation:
    • Enqueue x to q1 (assuming size of q1 is unlimited).
  2. pop(s) operation:
    • One by one dequeue everything except the last element from q1 and enqueue to q2.
    • Dequeue the last item of q1, the dequeued item is result, store it.
    • Swap the names of q1 and q2
    • Return the item stored in step 2.
       

       

      using System; 
      using System.Collections; 
      class GfG 
      { 
          public class Stack 
          { 
              public Queue q1 = new Queue(); 
              public Queue q2 = new Queue(); 
              //Just enqueue the new element to q1 
              public void Push(int x) => q1.Enqueue(x); 
       
              //move all elements from q1 to q2 except the rear of q1. 
              //Store the rear of q1 
              //swap q1 and q2 
              //return the stored result 
              public int Pop() 
              { 
                  if (q1.Count == 0) 
                      return -1; 
                  while (q1.Count > 1) 
                  { 
                      q2.Enqueue(q1.Dequeue()); 
                  } 
                  int res = (int)q1.Dequeue(); 
                  Queue temp = q1; 
                  q1 = q2; 
                  q2 = temp; 
                  return res; 
              } 
       
              public int Size() => q1.Count; 
       
              public int Top() 
              { 
                  if (q1.Count == 0) 
                      return -1; 
                  while (q1.Count > 1) 
                  { 
                      q2.Enqueue(q1.Dequeue()); 
                  } 
                  int res = (int)q1.Dequeue(); 
                  q2.Enqueue(res); 
                  Queue temp = q1; 
                  q1 = q2; 
                  q2 = temp; 
                  return res; 
              } 
          }; 
          public static void Main(String[] args) 
          { 
              Stack s = new Stack(); 
          s.Push(1); 
          Console.WriteLine("Size of Stack: " + s.Size() + "\tTop : " + s.Top()); 
          s.Push(7); 
          Console.WriteLine("Size of Stack: " + s.Size() + "\tTop : " + s.Top()); 
          s.Push(9); 
          Console.WriteLine("Size of Stack: " + s.Size() + "\tTop : " + s.Top()); 
       
          s.Pop(); 
          Console.WriteLine("Size of Stack: " + s.Size() + "\tTop : " + s.Top()); 
          s.Pop(); 
          Console.WriteLine("Size of Stack: " + s.Size() + "\tTop : " + s.Top()); 
       
          s.Push(5); 
          Console.WriteLine("Size of Stack: " + s.Size() + "\tTop : " + s.Top()); 
          } 
      } 
      //Submitted by Sakti Prasad 
       
      //Size of Stack: 1 Top : 1 
      //Size of Stack: 2 Top : 7 
      //Size of Stack: 3 Top : 9 
      //Size of Stack: 2 Top : 7 
      //Size of Stack: 1 Top : 1 
      //Size of Stack: 2 Top : 5 

      Output :

      current size: 4432current size:

Popular posts from this blog

Window function in PySpark with Joins example using 2 Dataframes (inner join)

-
Input details: #● File has json records #● Each record has fields: #○ user_id #○ card_num #○ merchant #○ category #○ amount #○ ts ### Below analysis to be done Sample data: +------+--------+---------+--------+----------+-------+|amount|card_num| category|merchant| ts|user_id|+------+--------+---------+--------+----------+-------+| 243| C_108| food| M_102|1579532902| U_104|| 699| C_106|cosmetics| M_103|1581759040| U_103|| 228| C_104| children| M_110|1584161986| U_103| Solution: from pyspark.sql.functions import col # this can be done without using window function creditCardData = spark.read.json(“card_transactions.json”) useridMaxSpendDF = df.groupby(‘user_id’).max(‘amount’) useridMaxSpendDF=useridMaxSpendDF.withColumnRenamed(“max(amount)”,”max_amount”) useridMaxSpendDF=useridMaxSpendDF.withColumnRenamed(“user_id”,”m_user_id”) cond = [creditCardData.user_id == useridMaxSpen...
Read more

Complex SQL: fetch the users who logged in consecutively 3 or more times (lead perfect example)

-
From the login_details table, fetch the users who logged in consecutively 3 or more times. Table Name : LOGIN_DETAILS Approach : We need to fetch users who have appeared 3 or more times consecutively in login details table. There is a window function which can be used to fetch data from the following record. Use that window function to compare the user name in current row with user name in the next row and in the row following the next row. If it matches then fetch those records. –Table Structure: drop table login_details; create table login_details( login_id int primary key, user_name varchar(50) not null, login_date date); delete from login_details; insert into login_details values (101, ‘Michael’, current_date), (102, ‘James’, current_date), (103, ‘Stewart’, current_date+1), (104, ‘Stewart’, current_date+1), (105, ‘Stewart’, current_date+1), (106, ‘Michael’, current_date+2), (107, ‘Michael’, cur...
Read more

Credit Card Data Analysis using PySpark (how to use auto broadcast join after disabling it)

-
Input details: #● File has json records #● Each record has fields: #○ user_id #○ card_num #○ merchant #○ category #○ amount #○ ts ### Below analysis to be done Sample data: +------+--------+---------+--------+----------+-------+|amount|card_num| category|merchant| ts|user_id|+------+--------+---------+--------+----------+-------+| 243| C_108| food| M_102|1579532902| U_104|| 699| C_106|cosmetics| M_103|1581759040| U_103|| 228| C_104| children| M_110|1584161986| U_103| Application: Here we will disable auto broadcast and then join 2 data frames and will see execution plan which should use broadcast join Solution: from pyspark.sql import SparkSession from pyspark.sql.functions import broadcast spark = SparkSession.builder.master(‘local[2]’)\ .appName(‘RDD_Methods_Examples’)\ .getOrCreate() print(spark.conf.get(“spark.sql.autoBroadcastJoinThreshold”)) spark.conf.set(“spark.sql.autoBroadcastJoinThreshold”, -1) pr...
Read more