Java Interview Questions for Intermediate

1.What is JVM? Why is Java called the “Platform Independent Programming Language”?

A Java virtual machine (JVM) is a process virtual machine that can execute Java bytecode. Each Java source file is compiled into a bytecode file, which is executed by the JVM. Java was designed to allow application programs to be built that could be run on any platform, without having to be rewritten or recompiled by the programmer for each separate platform. A Java virtual machine makes this possible, because it is aware of the specific instruction lengths and other particularities of the underlying hardware platform.

2.What does System.gc() and Runtime.gc() methods do?

These methods can be used as a hint to the JVM, in order to start a garbage collection. However, this it is up to the Java Virtual Machine (JVM) to start the garbage collection immediately or later in time.

3. Is Java “pass-by-reference” or “pass-by-value”?

Java is always pass-by-value. Unfortunately, when we pass the value of an object, we are passing the reference to it. There is no such thing as “pass-by-reference” in Java. This is confusing to beginners.

The key to understanding this is that something like

Dog myDog;

is not a Dog; it’s actually a pointer to a Dog.

So when you have

Dog myDog = new Dog("Rover");foo(myDog);

you’re essentially passing the address of the created Dog object to the foo method.

4.What is structure of Java Heap?

The JVM has a heap that is the runtime data area from which memory for all class instances and arrays is allocated. It is created at the JVM start-up. Heap memory for objects is reclaimed by an automatic memory management system which is known as a garbage collector. Heap memory consists of live and dead objects. Live objects are accessible by the application and will not be a subject of garbage collection. Dead objects are those which will never be accessible by the application, but have not been collected by the garbage collector yet. Such objects occupy the heap memory space until they are eventually collected by the garbage collector.

5. What is JIT?

The JIT is the JVM’s mechanism by which it can optimise code at runtime.

JIT means Just In Time. It is a central feature of any JVM. Among other optimisations, it can perform code inlining, lock coarsening or lock eliding, escape analysis etc.

The main benefit of the JIT is on the programmer’s side: code should be written so that it just works; if the code can be optimised at runtime, more often than not, the JIT will find a way.

6.What is the volatile keyword useful for?

volatile has semantics for memory visibility. Basically, the value of a volatile field becomes visible to all readers (other threads in particular) after a write operation completes on it. Without volatile, readers could see some non-updated value.

7.Compare Heaps vs Arrays to implement Priority Queue

Heap is generally preferred for priority queue implementation because heaps provide better performance compared arrays or linked lists:

In Array:
insert() operation can be implemented by adding an item at end of array in O(1) time.
getMax() operation can be implemented by linearly searching the highest priority item in array. This operation takes O(n) time.
deleteMax() operation can be implemented by first linearly searching an item, then removing the item by moving all subsequent items one position back.

In a Binary Heap:
getMax() can be implemented in O(1) time,
insert() can be implemented in O(log n) time and
deleteMax() can also be implemented in O(log n) time.

8.Convert a Binary Tree to a Doubly Linked List

This can be achieved by traversing the tree in the in-order manner that is, left the child -> root ->right node.

In an in-order traversal, first the left sub-tree is traversed, then the root is visited, and finally the right sub-tree is traversed.

One simple way of solving this problem is to start with an empty doubly linked list. While doing the in-order traversal of the binary tree, keep inserting each element output into the doubly linked list. But, if we look at the question carefully, the interviewer wants us to convert the binary tree to a doubly linked list in-place i.e. we should not create new nodes for the doubly linked list.

This problem can be solved recursively using a divide and conquer approach. Below is the algorithm specified.

Start with the root node and solve left and right sub-trees recursively
At each step, once left and right sub-trees have been processed:
- fuse output of left subtree with root to make the intermediate result
- fuse intermediate result (built in the previous step) with output from the right sub-tree to make the final result of the current recursive call

Implementation:

public static void BinaryTreeToDLL(Node root) {    if (root == null)        return;    BinaryTreeToDLL(root.left);    if (prev == null) { // first node in list        head = root;    } else {        prev.right = root;        root.left = prev;    }    prev = root;    BinaryTreeToDLL(root.right);    if (prev.right == null) { // last node in list        head.left = prev;        prev.right = head;    }}

9.What is complexity of Hash Table?

Hash tables are O(1) average and amortized time complexity case complexity, however it suffers from O(n) worst case time complexity (when you have only one bucket in the hash table, then the search complexity is O(n)). A hashtable typically has a space complexity of O(n).

Hash tables suffer from O(n) worst time complexity due to two reasons:

If too many elements were hashed into the same key: looking inside this key may take O(n) time (for linked lists)
Once a hash table has passed its load balance – it has to rehash (create a new bigger table, and re-insert each element to the table).

However, it is said to be O(1) average and amortized case because:

It is very rare that many items will be hashed to the same key if you chose a good hash function and you don’t have too big load balance.
The rehash operation, which is O(n), can at most happen after n/2 ops, which are all assumed O(1): Thus when you sum the average time per op, you get : (n*O(1) + O(n)) / n) = O(1)

10.Check if parentheses are balanced using Stack

One of the most important applications of stacks is to check if the parentheses are balanced in a given expression. The compiler generates an error if the parentheses are not matched.

Here are some of the balanced and unbalanced expressions:

Algorithm

Declare a character stack which will hold an array of all the opening parenthesis.
Now traverse the expression string exp.
If the current character is a starting bracket (( or { or [) then push it to stack.
If the current character is a closing bracket () or } or ]) then pop from stack and if the popped character is the matching starting bracket then fine else parenthesis are not balanced.
After complete traversal, if there is some starting bracket left in stack then “not balanced”

We are traversing through each character of string, Time complexity O(n).
We are storing the opposite parentheses characters in the stack, in the worst case there can be all the opposite characters in the string, Space complexity O(n).

Implementation:

public static boolean balancedParenthensies(String s) {    Stack<Character> stack  = new Stack<Character>();    for(int i = 0; i < s.length(); i++) {        char c = s.charAt(i);        if(c == '[' || c == '(' || c == '{' ) {                 stack.push(c);        } else if(c == ']') {            if(stack.isEmpty() || stack.pop() != '[') {                return false;            }        } else if(c == ')') {            if(stack.isEmpty() || stack.pop() != '(') {                return false;            }                   } else if(c == '}') {            if(stack.isEmpty() || stack.pop() != '{') {                return false;            }        }    }    return stack.isEmpty();}

11.Explain how Heap Sort works?

Heapsort is a comparison-based sorting algorithm. Heapsort can be thought of as an improved selection sort: like that algorithm, it divides its input into a sorted and an unsorted region, and it iteratively shrinks the unsorted region by extracting the largest element and moving that to the sorted region. The improvement consists of the use of a heap data structure rather than a linear-time search to find the maximum.

A heap is a complete binary tree (every level filled as much as possible beginning at the left side of the tree) that follows this condition: the value of a parent element is always greater than the values of its left and right child elements. So, by taking advantage of this property, we can pop off the max of the heap repeatedly and establish a sorted array.

In an array representation of a heap binary tree, this essentially means that for a parent element with an index of i, its value must be greater than its left child [2i+1] and right child [2i+2] (if it has one).

The HeapSort steps are:

Create a max heap from the unsorted list
Swap the max element, located at the root, with the last element
Re-heapify or rebalance the array again to establish the max heap order. The new root is likely not in its correct place.
Repeat Steps 2–3 until complete (when the list size is 1)

Best: O(n log n)
Average: O(n log n)
Worst: O(n log n)

12.How to merge two sorted Arrays into a Sorted Array?

Let’s look at the merge principle:

Given two separate lists A and B ordered from least to greatest, construct a list C by:

repeatedly comparing the least value of A to the least value of B,
removing (or moving a pointer) the lesser value, and appending it onto C.
when one list is exhausted, append the remaining items in the other list onto C in order.
The list C is then also a sorted list.

Complexity Analysis: O(n)

Implementation:

public static int[] merge(int[] a, int[] b) {    int[] answer = new int[a.length + b.length];    int i = 0, j = 0, k = 0;    while (i < a.length && j < b.length)         answer[k++] = a[i] < b[j] ? a[i++] :  b[j++];    while (i < a.length)          answer[k++] = a[i++];    while (j < b.length)            answer[k++] = b[j++];    return answer;}

13.How can Hash Functions be used to perform lookups?

Searching through large quantities of data is a very resource-intensive process. Imagine you’ve got a table listing every inhabitant of a big city, with lots of different fields for each entry (first name, second name, address, etc.). Finding just one term would be very time-consuming and require a lot of computing power. To simplify the process, each entry in the table can be converted into a unique hash value. The search term is then converted to a hash value. This limits the number of letters, digits and symbols that have to be compared, which is much more efficient than searching every field that exists in the data table.

14.What is Hash Collision?

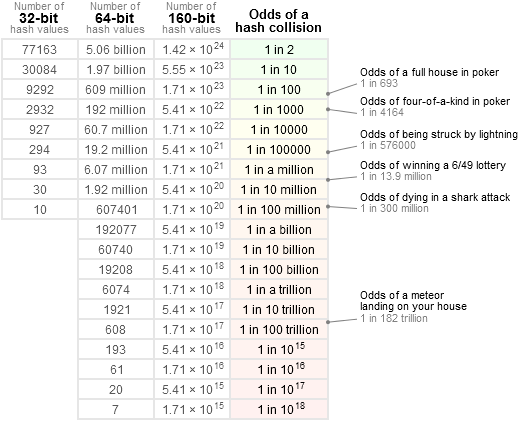
There’s always a chance that two different inputs for hash function will generate the same hash value. This is known as a hash collision. If a collision happens, you just compare the actual objects you are hashing to see if they match. What is the probability of a hash collision? This question is just a general form of the birthday problem from mathematics:

Given k randomly generated values, where each value is a non-negative integer less than N, what is the probability that at least two of them are equal?

Take the well-known hash function CRC32, for example. If you feed this function the two strings “plumless” and “buckeroo”, it generates the same value. This is known as a hash collision.

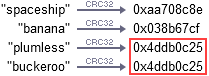
Assuming your hash values are 32-bit, 64-bit or 160-bit, the following table contains a range of small probabilities:

15.What is MD5?

MD5 is a so-called cryptographic hash function. Although MD5 was initially designed to be used as a cryptographic hash function, it has been found to suffer from extensive vulnerabilities. It can still be used as a checksum to verify data integrity, but only against unintentional corruption.

This basically means that you can give in any bitstring as input for the function, and you will get out a fixed-size bitstring (128-bit in the case of MD5) as output. The output is usually called “digest”.

The digest depends solely on the input and nothing else. Thus in itself it can be used as an integrity proof, but not as authenticity, if the underlying hash function has the necessary properties . This means that for two different outputs the digest itself should be also different. The problem is that the digest’s size is fixed, which in turn means that with sufficient number of messages it will always be possible to find a collision (i.e., two different inputs yielding the same output).

One should also note that there is nowadays no justification to use MD5, as weaknesses have been discovered (namely post-fix collision attacks). Also using SHA-256/512 on modern hardware is usually faster then MD5.

Tech Studio Online